一般教育
一般教育


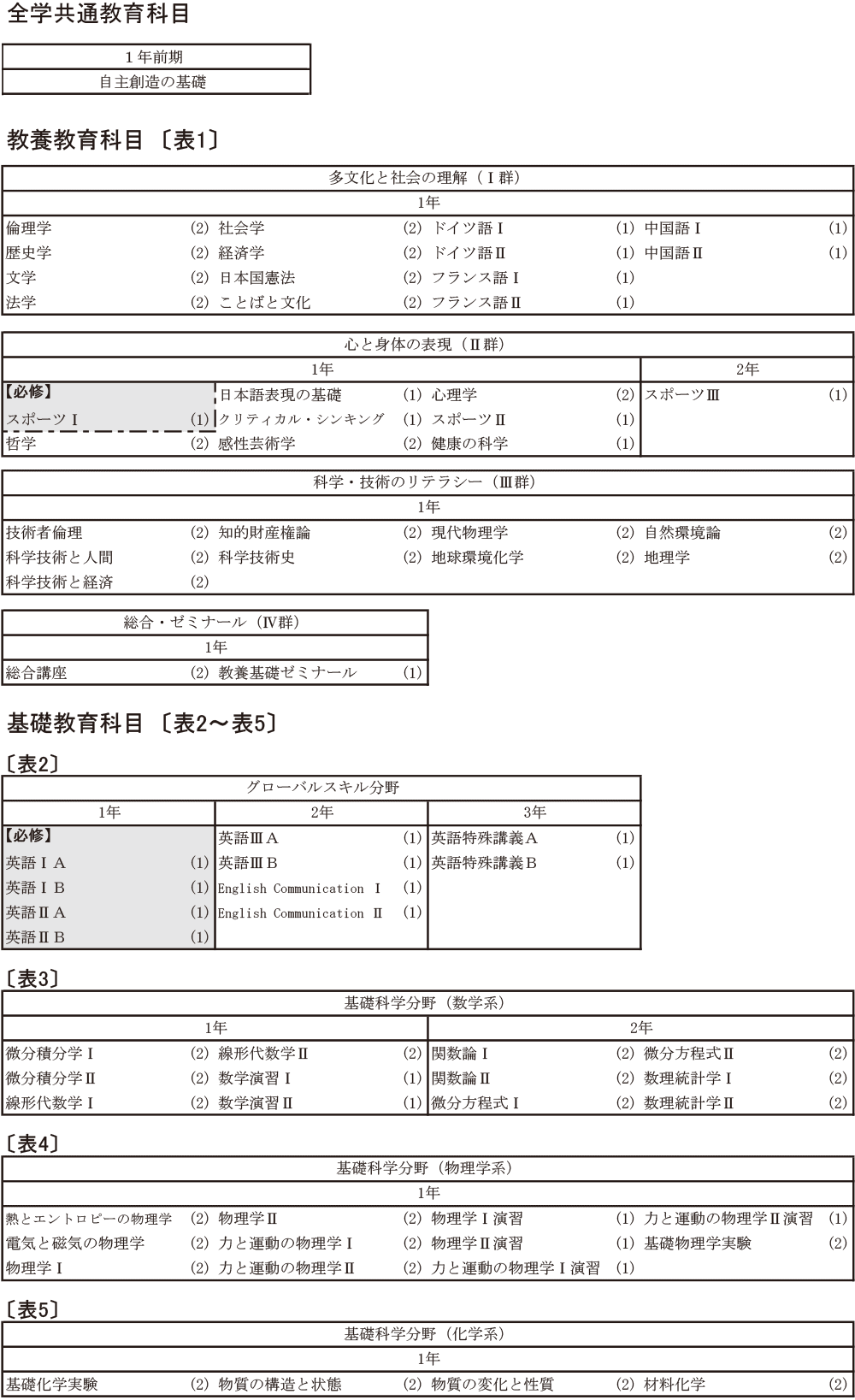
日本大学理工学部では、すべての学科の学生を対象に一般教育(共通科目)を設置しています。
共通科目は「教養教育科目」「外国語科目」「保健体育科目」「基礎教育科目」で構成され、主に1~2年生を対象に開講しています。
現代社会において、理工学の専門知識や技術が社会の創造と発展には不可欠な要素となっています。
一般教育教室では、現代社会の要請に応えられるしっかりとした基礎学力や専門知識、技術を身につけ、培った能力を最大限に生かす方法や態度を学ぶ場を数多く用意しています。「生きるための知恵」を学び、個々の学問領域の枠組みにとらわれない、柔軟な発想と知の総合力を身につけましょう。

「教養」を磨くって何をすること?
「何をつくり、それをどうマネジメントしていくか」を共に考え、互いの「夢」を表現し、批評しあうパートナーシップの時代には、「教養」がますます必要になります。
それでは、教養を磨くとは何をすることでしょう?
- (1)多角的な分析手法......
複眼的なものの見方を身につける - 人間とはどんな存在で、社会はどう動いていくのかを考えるには、自然科学や数理的なものの見方だけでなく、人文学(哲学、倫理学、歴史学、文学など)や、社会科学(法学、経済学、経営学、社会学、心理学など)の分析手法から生まれる、ものの見方を身につける必要があります。
- (2)対話力......
専門知識を生かす「共創力」を身につける - 分析によって得た多数の仮説を総合的に判断し、多くの人々を巻き込んで豊かな環境をデザインしていくためには、共創のための対話力、表現力、批評力、語学力などを磨く必要があります。


少人数制のゼミナール
&総合講座
- (1)教養ゼミナール
-
教養ゼミナールでは、教員が一方的に講義するのではなく、学生自身が調べたこと、体験したこと、考えたことなどを発表したり、議論したりすることを主とします(これをアクティブラーニングといいます)。少人数クラスなので、普段の授業よりも学生と教員との間の距 離が縮まります。教員が専門性を生かし多様なテーマを設定しますが、すぐに役立つことよりも、皆さんの視野を広げ、長い人生で糧となることを学びます。授業を通して、広く興味を持ち、自主的に学習する能力やプレゼンテーションをする力を養います。実際の授業の様子を「『宇宙の物理』入門」を例に取ってみてみましょう。この授業では、宇宙物理に関する入門的教科書を選び読んでいきます。
数式を確認し、わからないところを調べ、本の内容を理解していきます。
これを一人で行うのは大変なので、互いに協力しながら進めます。例えば、報告者が担当ページの内容を発表し、ほかの学生はわからなかったことを質問し、報告者はその質問に答えます。時には教員が助け舟を出すこともあります。こうして宇宙の物理についての理解を深めるとともに、学問のための基本作法を身につけていきます。
- (2)総合講座
-
現代社会においては、国際的視野に立った総合的な判断力に基づく思考・行動が求められています。
総合講座では、複数の教員による異なる学問領域からの問題提起を受け、学生一人ひとりが事象を総合的にとらえて問題点を発見し、自らの力で解決する能力を獲得することをめざしています。2017年度は「環境と人間」「言語と社会」「人工知能との共生のかたちを考える」を開講します。
研究一覧※ 研究者情報データベースを表示するには、名前をクリックして下さい。
人文社会科学系列
-
倫理学・技術者倫理
- 〈経験と言語形式の連関〉と〈文化・社会形態〉の相互作用に関するシステム論的研究
-
憲法
- 受信料制度と知る自由、自衛権、地方自治
-
日本近代文学
- 田山花袋・島崎藤村等の作品研究
-
藤木 秀明 助教官民連携(PPP)
- 地域における金融資源を活用した公共経営、PPP/PFI、SIB、PFS、公共施設マネジメント
数学系列
-
微分方程式論
- 各種境界値問題に対するグリーン関数の解析的・代数的構造の究明、再生核を利用した連続・離散ソボレフ不等式の最良評価
-
常微分方程式論
- 常微分方程式の解軌道の定性的理論
-
代数解析学
- 佐藤超函数、超局所解析、D加群
-
応用解析学
- 数値解析、シミュレーション解析
-
偏微分方程式論
- 非線形放物型方程式の解の長時間挙動および爆発問題
-
代数解析学
- 多変数ラプラス超関数の理論
-
確率過程論
- ランダム媒質中のランダムウォークの漸近挙動について
-
実解析・調和解析
- 実解析・調和解析的手法による掛谷問題の研究
-
代数幾何学
- K3曲面上のベクトル束、曲線のブリルネーター理論とその周辺
-
多変数関数論
- 不変計量を用いた正則同値問題の研究
-
内田 匠風 助教微分方程式論
- 完全WKB解析、特異摂動の代数解析
物理系列
-
相対論・宇宙論
- 時空特異点およびブラックホールの物理
-
磁性体物理・物理教育
- 教育教材の開発
-
統計物理学
- スピン系、場の理論、くりこみ群
-
分子科学・反応動力学
- 光と物質の相互作用、少数量子多体系
-
統計力学・複雑系科学
- カタストロフ複雑系現象としての地震
-
物性物理学
- パターン形成、破壊制御、レオロジー
-
固体物理・教育
- 磁性、理科教育機材、書籍撮影装置
-
原子分子物理学
- 原子分子およびその集合体の衝突過程とその星間物理化学への応用
-
一般相対論
- 重力場方程式の厳密解の構成とその応用
-
固体物性・物理教育
- 機能性電子材料の探索と評価
-
統計物理学
- 数理地形、生物物理、複雑系
化学系列
-
無機材料化学
- 産業副産物の有用再資源化
-
分析化学・環境化学
- 超微量元素の分離および分析手法の開発
-
物理化学・触媒化学
- 固体触媒、環境浄化、金属ナノ粒子、担体改質、自己組織化、水溶媒
-
材料化学
- 新規セメント系材料の開発
-
有機化学
- 環境低負荷型有機合成反応の開発
-
材料化学
- セメント系材料の水和反応
-
分析化学
- 有害物質除去法の開発
-
天然物化学
- 理科教育、有用天然物の探索
-
物理化学・計算機化学
- 溶液中の分子のダイナミクスに関する研究
地学系列
-
自然地理学、
地形学 - 氷河地形、気候変動、GIS、リモートセンシング、地学教育
英語系列
-
19世紀アメリカ文学
- マーク・トウェインの晩年思想
-
言語学・生成文法理論
- 英語と日本語を中心とした比較統語論
-
英文学
- ポストコロニアル文学研究
-
17世紀英文学
- 形而上詩人の奇想、宗教上のスタンス
-
アメリカ文化論・教育工学
- アメリカの人種・民族・宗教と文学、教学IR
-
英語教育
- 教育学英語教授法とカリキュラム
-
英語教育・教育心理学
- 英語学習意欲
-
英文学・英米児童文学
- ジョン・ミルトン研究、英米児童文学
-
アメリカ文学・文化論
- ハーマン・メルヴィル研究を中心に
初修外国語系列
-
社会言語学
- 言語政策研究、批判的談話研究、ポピュリズム研究、地域研究(ベルギー)
-
日中外交史、中国語学
- 日清戦争史、中国語教授法
-
現代ドイツ語学
- ドイツ語の語順と文構造
-
現代ドイツ文法
- 日独対照形容詞研究
体育系列
-
スポーツ心理学
- エキスパートの熟達化とコーチング
-
スポーツ生理学
- 身体活動習慣・生活習慣と体力の関係
-
運動生理学
- 運動制御と脳活動
-
スポーツ生理学
- 幼児期の発育・発達と運動能力について
-
体育測定評価学
- 成長期のスポーツ傷害予防、ストレングス&コンディショニング
-
鈴木 功士 助教スポーツ工学
- スポーツ流体、競技用ウエア
-
コーチング学
- 水泳競技におけるコーチング
教職系列
-
教育思想史
- シュタイナーの教育思想、教育メディア研究
-
学校教育学
- 日米の学校改革、ジェンダーと教育
-
大越 健斗 助教学校教育学
- 数学教育、教師の信念
学芸員系列
-
服飾美学、博物館学
- 色彩と紋様の象徴性、技術と道具史、資料保存、修復、復元